Investigating Innovative Experimental Curricular Approaches to Enhance Conceptual Development in Mathematics Education
Main Article Content
Abstract
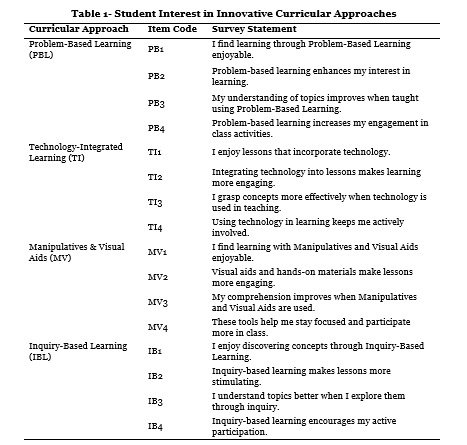
Purpose – Mathematics education is increasingly shifting from rote memorization to approaches that foster conceptual understanding. In Ghana, however, traditional methods still dominate, limiting students' ability to apply mathematical concepts effectively. This study investigates the impact of active learning strategies—Problem-Based Learning (PBL), Inquiry-Based Learning (IBL), manipulatives, and technology integration—on students’ conceptual understanding of mathematics within a sub-Saharan African context.
Methodology – A quantitative design was employed, involving 300 students from the Ejisu-Juaben Municipality in Ghana, selected through stratified random sampling. Data were collected using structured questionnaires and analyzed statistically to assess the relationship between instructional strategies and conceptual learning outcomes.
Findings – The results indicate that technology integration had the strongest positive effect on students’ comprehension and engagement. PBL also improved learning outcomes but required additional instructional support. Both IBL and the use of manipulatives contributed moderately to conceptual understanding.
Novelty – This study offers a novel contribution by addressing an underrepresented region in educational research. It is among the first to examine the combined effects of multiple active learning strategies in a sub-Saharan African setting, with a specific focus on conceptual understanding rather than performance metrics.
Significance – The findings provide actionable insights for educators and policymakers in developing contexts, emphasizing the importance of adopting technology-enhanced and student-centered approaches to improve mathematics instruction and deepen students’ problem-solving abilities.
Article Details
References
Adu-Gyamfi, K. (2016). Challenges in teaching and learning mathematics in basic schools in Ghana. Journal of Education and Practice, 7(3), 62-66.
Anamuah-Mensah, J., Mereku, D. K., & Ghartey, J. (2008). Ghanaian junior secondary school students' achievement in mathematics and science: Results from Ghana's participation in the 2007 Trends in International Mathematics and Science Study. International Journal of Educational Development, 28(3), 277-282.
Barrows, H. S. (1996). Problem-based learning in medicine and beyond: A brief overview. New Directions for Teaching and Learning, 1996(68), 3-12.
Boaler, J. (2016). Mathematical mindsets: Unleashing students' potential through creative math, inspiring messages and innovative teaching. Jossey-Bass.
Braun, V., & Clarke, V. (2006). Using thematic analysis in psychology. Qualitative Research in Psychology, 3(2), 77-101.
Bransford, J. D., Brown, A. L., & Cocking, R. R. (Eds.). (2000). How people learn: Brain, mind, experience, and school. National Academy Press.
Carbonneau, K. J., Marley, S. C., & Selig, J. P. (2013). A meta-analysis of the efficacy of teaching mathematics with concrete manipulatives. Journal of Educational Psychology, 105(2), 380-400.
Clements, D. H., & Sarama, J. (2011). Early childhood teacher education: The case of mathematics. Journal of Early Childhood Teacher Education, 32(3), 231-244.
Creswell, J. W., & Plano Clark, V. L. (2011). Designing and conducting mixed methods research. Sage.
Cuban, L. (2013). Inside the black box of classroom practice: Change without reform in American education. Harvard Education Press.
Dillman, D. A., Smyth, J. D., & Christian, L. M. (2014). Internet, phone, mail, and mixed-mode surveys: The tailored design method. John Wiley & Sons.
Field, A. (2013). Discovering statistics using IBM SPSS statistics. Sage.
Fosnot, C. T. (2005). Constructivism: Theory, perspectives, and practice. Teachers College Press.
Fullan, M. (2007). The new meaning of educational change. Teachers College Press.
Gravemeijer, K. P. E. (1999). How emergent models may foster the constitution of formal mathematics. Mathematical Thinking and Learning, 1(2), 155-177.
Hiebert, J., Carpenter, T. P., Fennema, E., Fuson, K. C., Wearne, D., Murray, H., ... & Human, P. (1997). Making sense: Teaching and learning mathematics with understanding. Heinemann.
Hiebert, J., & Grouws, D. A. (2007). The effects of classroom mathematics teaching on students' learning. In F. K. Lester (Ed.), Second handbook of research on mathematics teaching and learning (pp. 371-404). Information Age Publishing.
Hmelo-Silver, C. E. (2004). Problem-based learning: What and how do students learn? Educational Psychology Review, 16(3), 235-266.
Kaput, J. J. (1992). Technology and mathematics education. In D. A. Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 515-556). Macmillan.
Kilpatrick, J., Swafford, J., & Findell, B. (Eds.). (2001). Adding it up: Helping children learn mathematics. National Academy Press.
Kvale, S., & Brinkmann, S. (2009). Interviews: Learning the craft of qualitative research interviewing. Sage.
Loucks-Horsley, S., Love, N., Stiles, K. E., Mundry, S., & Hewson, P. W. (2003). Designing professional development for teachers of science and mathematics. Corwin Press.
Merriam, S. B. (2009). Qualitative research: A guide to design and implementation. Jossey-Bass.
National Research Council. (2001). Adding it up: Helping children learn mathematics. National Academy Press.
Nisa’, K., Nasrullah, A., Hidayat, A., Mahuda, I., & Bhat , I. A. (2023). Problem-Based Learning in Improving Problem-Solving Ability and Interest in Learning Mathematics: An Empirical Study. International Journal of Mathematics and Mathematics Education, 1(3), 206–217. https://doi.org/10.56855/ijmme.v1i3.725
Patton, M. Q. (2002). Qualitative research and evaluation methods. Sage.
Piaget, J. (1952). The origins of intelligence in children. International Universities Press.
Piaget, J. (1970). Science of education and the psychology of the child. Viking.
Resnick, L. B. (1987). Education and learning to think. National Academy Press.
Rittle-Johnson, B., & Koedinger, K. R. (2005). Designing knowledge scaffolds to support mathematical problem solving. Cognition and Instruction, 23(3), 313-349.
Rittle-Johnson, B., Siegler, R. S., & Alibali, M. W. (2001). Developing conceptual understanding and procedural skill in mathematics: An iterative process. Journal of Educational Psychology, 93(2), 346-362.
Schacter, J. (2001). The impact of education technology on student achievement: What the most current research has to say. Milken Exchange on Education Technology.
Schoenfeld, A. H. (2002). Making mathematics work for all children: Issues of standards, testing, and equity. Educational Researcher, 31(1), 13-25.
Sfard, A. (1991). On the dual nature of mathematical conceptions: Reflections on processes and objects as different sides of the same coin. Educational Studies in Mathematics, 22(1), 1-36.
Stigler, J. W., & Hiebert, J. (1999). The teaching gap: Best ideas from the world's teachers for improving education in the classroom. Free Press.
Sawyer, R. K. (2006). The Cambridge handbook of the learning sciences. Cambridge University Press.